Application of Graph – Minimum Spanning Tree
A subgraph T of a connected, undirected and weighted graph G(V, E) referred as Spanning Tree provided,
- Subgraph possesses all the vertices of the graph G(V, E)
- Subgraph is a tree
Spanning Tree
Every spanning tree will have an associated cost(sum of weights of all the edges). Spanning trees of a graph is shown below along with its associated cost. It could have more spanning trees also. Therefore a graph has several spanning trees and some might give same cost too.
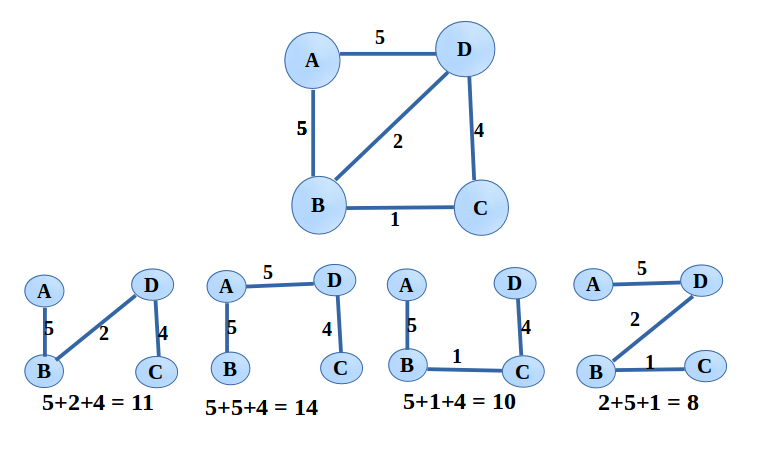
Minimum Spanning Tree(MST)
A spanning tree that costs least among all will be the minimum spanning tree. In other words, finding a min weight set of edges that connects all of the vertices. For the above graph, following are the minimum spanning trees,
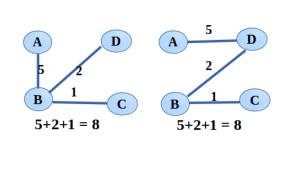
There are many situations, MST is required. Consider a telephone line, required to connect all the branches of a company. The path causes higher cost will not be selected. This is nothing but minimum spanning tree problem. See the application section, for other applications.
The two widely used famous algorithms are
- Prim’s algorithm
- Kruskal’s algorithm
Both algorithms are of greedy approach and give the same output.
1. Kruskal’s algorithm:
The idea of this algorithm is,
First sort the edges(weight) of the graph in non-decreasing order. From the sorted list, starts with first one, then add next one and so on accordingly. And as MST is a tree, therefore, every time an edge is added, the cycle should not be formed.
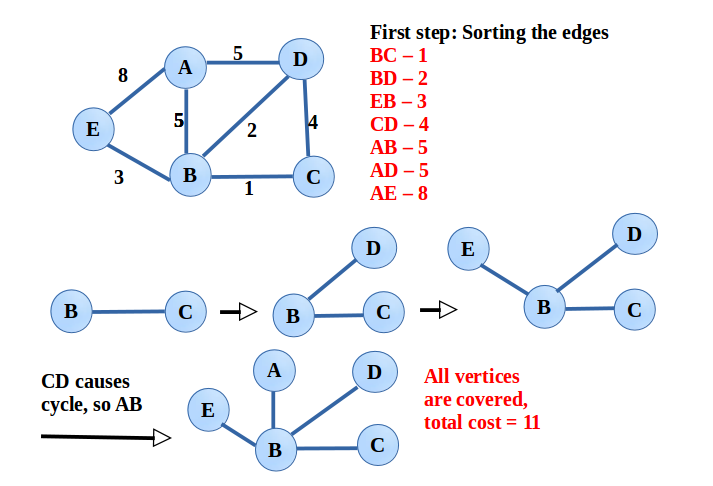
Graphical representation of Kruskal’s algorithm.
2. Prim’s algorithm:
The idea of this algorithm is
Start with any vertex(say A) of the graph G(V, E), to build a tree T. Add the least cost edge to the tree T provided one of the endpoints of that edge must be in T. Add the edges until all the vertices are covered. Same here also, the cycle should not be formed on adding an edge.
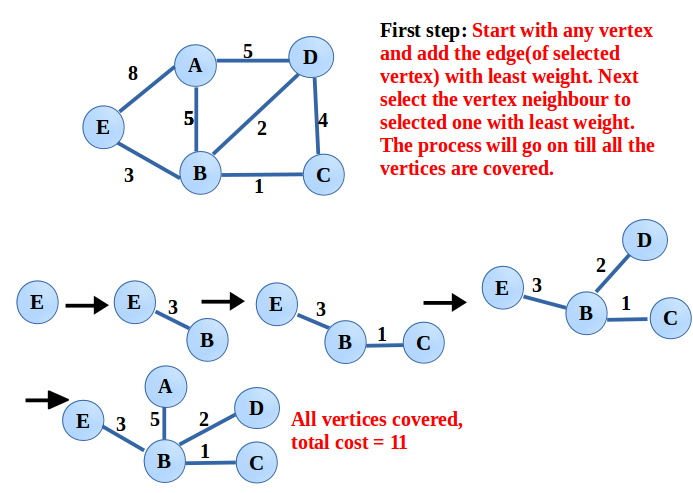
Application:
- Cluster analysis
- Image segmentation
- Handwriting recognition
- Medical Image Processing
- Identify patterns in gene expression
- Approximation to NP hard problems
- Document categorization for web search
- Network design for telephone, electrical, hydraulic, TV cable, computer, road etc.
- There are many indirect applications also.
So that’s all for this tutorial. Hope this helps and you like the tutorial. Do ask for any queries in the comment box and provide your valuable feedback.
Do not forget to SHARE and SUBSCRIBE.
Keep Coding!! Happy Coding!! 🙂
