Binary Tree – Introduction, Explanation and Implementation

A specialized form of tree data structure in which each node can have at most two children, such a tree is referred as a Binary Tree.

The Topmost node is called root node. The two children are referred as Left and Right child. The node with no child is referred as leaf node.

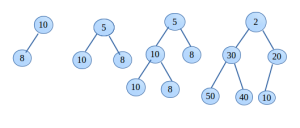
In above image, 2, 5 and 8 are the roots of their respective trees and 79, 20, and (68, 50, 10) are leaves respectively.

Types of Binary Tree:

Binary tree can be classified based on its structure,

1. Complete binary tree, if all the levels are completely filled except possibly the last level and the nodes in the last level are as left as possible. In other words, a binary tree where nodes are filled like left to right at each depth(top to down).

   

2. Full binary tree, All the nodes in such a binary tree possesses either 0 or 2 children.

   

3. Perfect binary tree
   • It must be a Full binary tree
   • All the leaves must be at the same level

     

Note:-

•  Full binary tree and Perfect binary tree, have no any standard definition. The aforementioned definition is more widely preferred.
• There are some lesser known types also such as incomplete binary tree, strict binary tree, almost complete binary tree, degenerate tree etc.

Implementation:

1. For full binary tree and complete binary tree, array is used.
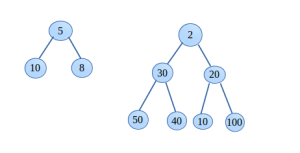
   See below, an array binTree[] of size 7 is created, each node of the shown binary tree is stored as root at index 0, left child of root at index 1 and so on. If the parent is at index i then left and right child at 2i and 2i+1 respectively.

   

2. Pointer based implementation,
   Under this, a node is created like we do for the linked list. There will be a structure that contains a key,  a pointer to the left subtree and a pointer to the right subtree.

   struct node {
       int key;
       struct node *left;
       struct node *right;
   };
   

Operation on Binary Tree:

The same known operation Insertion, Deletion, Searching, Traversal and some others are applied to the binary tree.
Howsoever, a binary tree is implemented with modification to have a more optimized operation. Binary Search Tree(BST), Balanced BST are some of the modified binary trees.
Thus, operations on binary tree are more emphasized on BST and Balanced BST rather than plainly applying on it.

Properties:

Q1) What are the maximum number of nodes in a binary tree of height h(that is a perfect binary tree)?
Ans) For height h – maximum number of noder are 2^(h+1) -1, where height of the leaf node is zero

Q2) What is the relationship between leaf node and an internal node?
Ans) In a binary tree, the number of leaf node is always one more than the number of internal nodes with two children.

Q3) What is the height of a complete binary tree?
Ans) Height of tree = ⌊logn⌋, where n is the total number of nodes

Q4) What is the number of internal nodes in a tree?
Ans) Internal nodes = ⌊(n/2)⌋ + 1 to n, where n is the total number of nodes

Applications:

• Heap tree, used to implement priority queue, and in dynamic memory allocation
• Huffman coding used in compression/decompression
• Syntax tree(compiler)

Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂

Recommended -