A tutorial on Dynamic Programming (DP) Approach
Dynamic programming is one of the algorithmic paradigm that solves many problems that are failed under other paradigms such as Divide and Conquer, Greedy approach etc.
The idea is to break the problem into smaller problems (call it sub problems) like we do in divide & conquer and then, find out the repeated sub problems. All the computed subproblems will be reused whenever repetition is there. Let’s understand it in part by part.
Declaring a Problem as a Dynamic Programming problem
A problem is categorized under Dynamic Programming Approach if it has,
1. Problem substructure
The problem can be divided into many sub problems. Merge sort and Quick sort breaks the problems into subproblems. Each distinct sub problem is solved independently and together they lead to the main problem.
For example, sub problems of mergeSort(arr[], 10) are
– mergeSort(arr[], 5), mergeSort(arr[], 5), mergeSort(arr[], 3), mergeSort(arr[], 2), mergeSort(arr[], 1), mergeSort(arr[], 2)
2. Overlapping Subproblems
This is the important step to take note of. There should be repeated sub problems and we’ll build a table to memorize each distinct sub problem so as not to compute again.
Merge sort and Quick sort do have sub problems but none is repeated i.e. their subproblems are different every time. Hence, these are not categorized under dynamic programming (DP).
Some problems of Dynamic Programming approach,
Problem1:
Finding Nth Fibonacci number{0, 1, 2, 3, 5, 8, 13…}
As every Nth Fibonacci no. is the sum of N-1th and N-2th Fibonacci no., therefore for N = 6, it would be computed as,
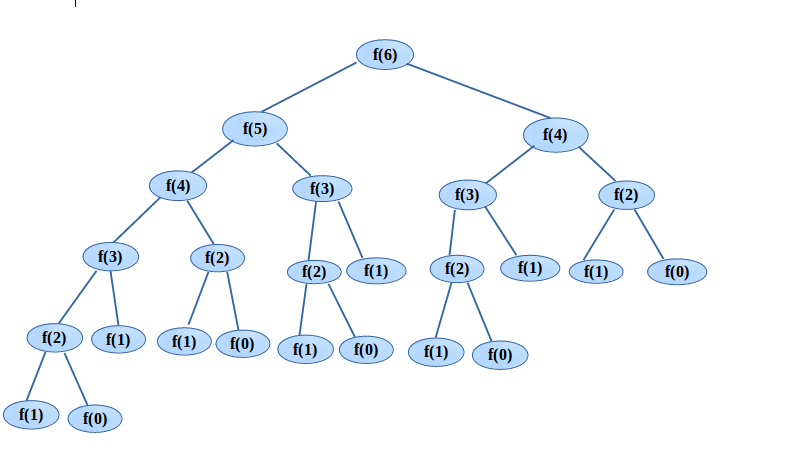
f(4) – computed 2 times
f(3) – computed 3 times
f(2) – computed 5 times
f(1) – computed 8 times
f(0) – computed 5 times
There are a number of repeated sub problems.
Here, the problem is broken into two sub problems which further broken into two sub problems by each. Hence, problem substructure is there. Also, many sub problems are repeated and that’s overlapping. The second condition is matched.
Thus, the problem is categorized under dynamic programming.
Problem2:
Subset sum problem: Given a set of number {1, 3, 4, 6, 9}, find out if there is a subset whose summation equals to M = 8.
The very simple approach would be either an element would be present or absent in the desired subset. Unfortunately, that would take O(2n), where n is the number of elements. Let’s try with dynamic programming,
Problem substructure: The problem could be broken down into smaller problems. Like start with smaller subsets as {1}, {3}, {4}…then, taking 2 elements at a time{1, 3}, {1, 4}, {3, 4}….then, three at a time and so on.
Overlapping subproblems: Finding the repeated ones, like once it’s found subset {9} is greater than M, then, every time a subset includes element 9, reject it immediately e.g. {1, 9}, {1, 3, 9}. Therefore, this problem has overlapping subproblems as well. Thus, the subset sum problem is a DP problem.
Approaches to solve a DP problems:
There are 2 approaches to solve a DP problem –
1. Top down DP
In this approach, a recursive call is made with the given problem size and next call is made with the smaller subproblem (argument value gets decreased) and further calls will be smaller than the previous ones just like calls in the Fibonacci series as shown above.
Once smallest subproblem is computed, then, its result will be used for the next calling. It’s comparatively easy to think and codes look simple, but, memory consumption is high and written codes are difficult to understand for a reader. This is referred as Memoization Method.
2. Bottom up DP
In this approach, rather than beginning with the main problem, start solving with the smallest one and on the way increase the subproblem size through using the computed sub problems. It’s based on iteration rather than recursion. It’s difficult to think, but, it’s easy for a reader to understand and also, memory consumption is less. Therefore, it’s more suggested to use. This is referred as Tabulization Method.
Popularly known problems in DP:
Floyd Warshall Algo,
Subset Sum Problem,
Knapsack 0/1 Problem,
Longest Common Subsequence
Longest Increasing Subsequence
Optimal Binary Search Tree
Counting Boolean Parenthesization
Matrix Chain Multiplication
Minimum Partitioning
Partition Problem
Rod Cutting
We will be discussing them in future posts, so stay tuned.
Share this to motivate us to keep writing such online tutorials and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂