Bubble Sort Algorithm and its Implementations

Bubble sort is the basic sorting algorithm which continuously compares the adjacent pairs and swaps them if they are in wrong order.

This algorithm is generally used to introduce algorithmic concepts to a beginner or is used in cases when the input list or array is almost sorted and have only a few elements misplaced from their actual location and that too at nearby locations.

Comparing to other simple O(n²) sorting algorithms like selection and insertion sort, bubble sort takes too many resources and time, hence its performance is not appropriate. In general, we prefer to use insertion sort and sometimes selection over Bubble sort algorithm.

The basic idea is that in first iteration of this algorithm we are able to move the largest element at the end of the list, in second iteration- second largest element at second last position in list and so on. Basically like selection sort it also divides the array into two parts of sorted and unsorted array and after each iteration we add the largest element from the unsorted array to the top of sorted array.

Let’s understand it with an example-

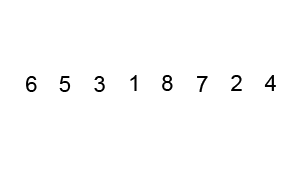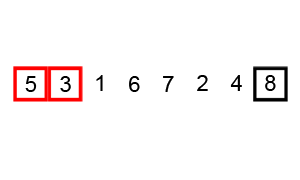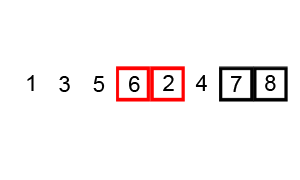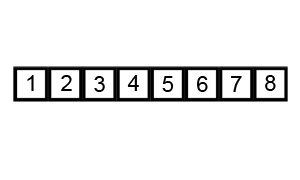
So in the above picture we can see that in each iteration we continuously check adjacent elements and shift the bigger one towards the end of the list and finally the largest element is placed at the end and we continue this iteration until we sort our complete list.

For the array of numbers “5 1 4 2 8”, let’s sort the array from lowest number to the greatest number using bubble sort. In each step, elements written in bold are being compared.

Example:
First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, the algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) –> ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) –> ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), the algorithm does not swap them.

Second Pass:
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.

Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

Iterative Pseudocode:

function bubblesort( var a as array )
    for i from 1 to N
        for j from 0 to N - 1
           if a[j] > a[j + 1]
              swap( a[j], a[j + 1] )
end function

• Iterative implementation in C
• Iterative implementation in Java

Optimized Pseudocode:

In optimized approach we use keep track and check is there any iteration in which no element is swapped and if this happens then it implies that the list is sorted and this situation is tracked by isSorted variable in our code as below.

function bubblesort2( var a as array )
    for i from 2 to N
        isSorted = true
        for j from 0 to N - 2
           if a[j] > a[j + 1]
              swap( a[j], a[j + 1] )
              isSorted = false
        if isSorted == true
            break
end function

• Optimized implementation in C
• Optimized implementation in Java

Asymptotic Analysis

Since this algorithm contains two nested loops and the number of comparisons is not dependent on the values of array items, so the complexity of this algorithm is O(n²). Summarizing all this –

Data structure used -> Array
Time Complexity (Best, worst and average case) -> O(n²)
Worst case space complexity -> O(n) total space, O(1) Auxiliary space

ITERATIVE Implementation of Bubble Sort in C programming language

// C program for implementation of Bubble sort
#include <stdio.h>

void swap(int *xp, int *yp)
{
    int temp = *xp;
    *xp = *yp;
    *yp = temp;
}

// A function to implement bubble sort
void bubbleSort(int arr[], int n)
{
   int i, j;
   for (i = 0; i < n-1; i++)
       for (j = 0; j < n-i-1; j++) //Last i elements are already in place
           if (arr[j] > arr[j+1])
              swap(&arr[j], &arr[j+1]);
}

/* Function to print an array */
void printArray(int arr[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", arr[i]);
    printf("
");
}

// Driver program to test above functions
int main()
{
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    bubbleSort(arr, n);
    printf("Sorted array: 
");
    printArray(arr, n);
    return 0;
}

Output:-

Sorted array:
11 12 22 25 34 64 90

ITERATIVE Implementation of Bubble Sort in Java

package com.codingeek.algorithms.sorting;

public class BubbleSortAlgorithm {

	// Implementation of Bubble Sort
	static void bubblesort(Integer[] input) {
		for (int i = 0; i < input.length - 1; i++)
			for (int j = 0; j < input.length - 1; j++) {
				if (input[j].intValue() > input[j + 1].intValue()) {
					int temp = input[j];
					input[j] = input[j + 1];
					input[j + 1] = temp;
				}
			}
	}

	// Main method to launch the program
	public static void main(String[] args) {
		Integer[] input = { 64, 34, 25, 12, 22, 11, 90 };
		bubblesort(input);
		System.out.println("Sorted array:");
		for (Integer value : input)
			{
			System.out.print(value + " ");
			}
	}
}

Output:-

Sorted array:
11 12 22 25 34 64 90

Optimized Implementation of Bubble Sort in C

// Optimized implementation of Bubble sort
#include <stdio.h>
#include<stdbool.h> // To use bool variable in our code
void swap(int *xp, int *yp)
{
    int temp = *xp;
    *xp = *yp;
    *yp = temp;
}

// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
   int i, j;
   bool isSorted;
   for (i = 0; i < n-1; i++)
   {
     isSorted = true;
     for (j = 0; j < n-i-1; j++)
     {
        if (arr[j] > arr[j+1])
        {
           swap(&arr[j], &arr[j+1]);
           isSorted = false;
        }
     }

     // IF no two elements were swapped by inner loop, then break
     if (isSorted)
        break;
   }
}

/* Function to print an array */
void printArray(int arr[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", arr[i]);
    printf("
");
}

// Driver program to test above functions
int main()
{
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    bubbleSort(arr, n);
    printf("Sorted array: 
");
    printArray(arr, n);
    return 0;
}

Output:-

Sorted array:
11 12 22 25 34 64 90

Optimized Implementation of Bubble Sort in Java

package com.codingeek.algorithms.sorting;

public class BubbleSortAlgorithm {

	// Optimized Implementation of Bubble Sort
	static void optimizedBubblesort(Integer[] input) {
		for (int i = 0; i < input.length - 1; i++) {

			boolean isSorted = true;
			for (int j = 0; j < input.length - 1; j++) {
				if (input[j].intValue() > input[j + 1].intValue()) {
					int temp = input[j];
					input[j] = input[j + 1];
					input[j + 1] = temp;
					isSorted = false;
				}
			}
			if (isSorted) {
				break;
			}
		}
	}

	// Main method to launch the program
	public static void main(String[] args) {
		Integer[] input = { 64, 34, 25, 12, 22, 11, 90 };
		optimizedBubblesort(input);
		System.out.println("Sorted Array -");
		for (Integer value : input) {
			System.out.print(value + " ");
		}
	}
}

Output:-

Sorted array:
11 12 22 25 34 64 90

Do share the wisdom and motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.

Keep Learning.. Happy Learning.. 🙂

Recommended -