Insertion Sort Algorithm – Explanation, Complexity and Implementation
Insertion sort is a comparison based sorting algorithm which sorts the array by shifting elements one by one from an unsorted sub-array to the sorted subarray. With each iteration, an element from the input is pick and inserts in the sorted list at the correct location.
In insertion sort, Input data is divided into two subsections (1st i.e. Sorted section and 2nd i.e. Unsorted section). The basic idea is with each iteration one element from unsorted section is moved to the sorted section and in this way by the end of the iterations all elements move to the sorted section and our input data gets sorted.
Here are some key points of insertion sort algorithm –
- Insertion sort is preferably used when the number of elements is small because performance decreases with increase in input data size.
- It can also be useful when input array is almost sorted, only a few elements are misplaced in the complete big array.
- Insertion sort takes maximum time to sort if elements are sorted in reverse order. And it takes minimum time (Order of n) when elements are already sorted.
- It is a stable algorithm as it does not change the relative order of elements with equal keys.
- It is in place sorting algorithm which requires an O(1) amount of extra memory space.
- It is better than Selection or bubble sort in spite of having O(n*n) complexity.
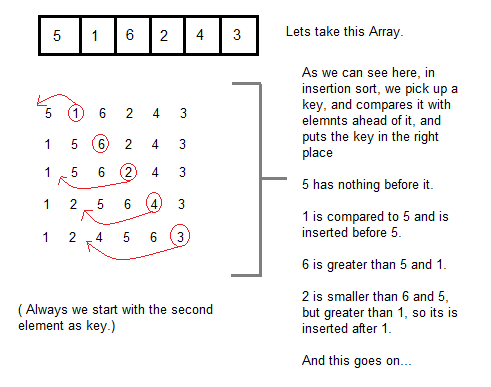
Let’s understand it with an example-
Since a picture speaks a thousand words. Just carefully read the steps in the image below and you will be able to visualize the concept of this algorithm.
Pseudocode of Insertion Sort
INSERTION-SORT(A)
for i = 1 to length(A)
key = A[i]
j = i - 1
while j >= 0 and A[j] > key
A[j+1] = A[j]
j = j - 1
end while
A[j+1] =
end for
Asymptotic Analysis
Since this algorithm contains two nested loops and the number of comparisons is not dependent on the values of array items, so the complexity of this algorithm is O(n2). Summarizing all this –
Worst Case Time complexity: O(n2)
Average Case Time complexity: O(n2)
Best Case Time complexity: O(n)
Space Complexity: O(1)
Data structure used->Array
Sorting In Place: Yes
Stable: Yes
ITERATIVE – Implementation of Insertion Sort in C programming language
#include <stdio.h>
#include <math.h>
/* Main function that performs insertion sorting. */
void insertionSort(int input[], int n){
int i, key, j;
for (i = 1; i < n; i++)
{
key = input[i];
j = i-1;
// Shifts elements to the correct location
// such that resulting inputay is a sorted one.
while (j >= 0 && input[j] > key)
{
input[j+1] = input[j];
j = j-1;
}
input[j+1] = key;
}
}
// A utility function ot print an inputay of size n
void printArray(int input[], int n){
int i;
printf("Sorted array - ");
for (i=0; i < n; i++)
printf("%d ", input[i]);
printf("
");
}
/* Driver program to test insertion sort */
int main(){
int input[] = {4, 10, 3, 1, 9, 15};
int n = sizeof(input)/sizeof(input[0]);
insertionSort(input, n);
printArray(input, n);
return 0;
}
Output:-
Sorted array - 1 3 4 9 10 15
ITERATIVE – Implementation of Insertion Sort in Java programming language
package com.codingeek.algorithms.sorting;
import java.util.Arrays;
public class InsertionSortAlgorithm {
public static void main(String[] args) {
final int[] input = { 4, 10, 3, 1, 9, 15 };
System.out.println("Before Sorting - " + Arrays.toString(input));
insertionSort(input);
System.out.println("After Sorting - " + Arrays.toString(input));
}
public static void insertionSort(int array[]) {
int n = array.length;
for (int j = 1; j < n; j++) {
int key = array[j];
int i = j-1;
while ( (i > -1) && ( array [i] > key ) ) {
array [i+1] = array [i];
i--;
}
array[i+1] = key;
}
}
}
Output:-
Before Sorting - [4, 10, 3, 1, 9, 15]
After Sorting - [1, 3, 4, 9, 10, 15]
RECURSIVE – Implementation of Insertion Sort in Java programming language
package com.codingeek.algorithms.sorting;
import java.util.Arrays;
class RecursiveInsertionSort{
public static void main(String[] args) {
final int[] input = { 4, 10, 3, 1, 9, 15 };
System.out.println("Before Sorting - " + Arrays.toString(input));
new RecursiveInsertionSort().sort(input, input.length);
System.out.println("After Sorting - " + Arrays.toString(input));
}
private int sort(int[] input, int maxIndex) {
if (maxIndex <= 1) {
return maxIndex;
}
maxIndex = sort(input, maxIndex - 1); // recursive call
// save a copy of the value in variable 'key'.
// This value will be placed in the correct position
// after the while loop below ends.
int key = input[maxIndex];
int i = maxIndex - 1;
// compare value in 'key' with all the elements in array
// that come before the element key.
while ((i >= 0) && (input[i] > key)) {
input[i+1] = input[i];
i--;
}
input[i+1] = key;
return maxIndex + 1;
}
}
Output:-
Before Sorting - [4, 10, 3, 1, 9, 15]
After Sorting - [1, 3, 4, 9, 10, 15]
That’s all for insertion sort, one of the most basic, simple and important sorting algorithms. As a developer, you should be aware of this algorithm and it is most likely to be asked about this algorithm in interviews as well. Although in the production code one must never use this algorithm because it has O(n*n) complexity. Always use merge sort or quick sort. In java use Collections.sort() method as it also uses mergesort internally( but now in newer java versions TimSort is being used).
Do share the wisdom and share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning.. Happy Learning.. 🙂
Thanks @Hitesh for simple explanation.