Quick Sort Algorithm –Explanation, Implementation, and Complexity

Quick Sort also uses divide and conquer technique like merge sort, but does not require additional storage space. It is one of the most famous comparison based sorting algorithm which is also called as partition exchange sort. Like merge sort, it also uses recursive call for sorting elements.

In Quick Sort pivot element is chosen and partition the array such that all elements smaller than pivot are arranged to left of pivot and element bigger than pivot are arranged to its right.
There are various ways to choose pivot element:

1. Chose pivot as first element.
2. Chose pivot as end element.
3. Chose pivot as median element.
4. Chose pivot as random element.

Here are some key points of quick sort algorithm –

• Quick Sort is also a good example of a recursive algorithm.
• We can express time complexity of quick sort by this recurrence relation:
  T(n) = T(k) + T(n-k-1)+ ?(n).
  T(k) -> recursion relation for elements left of pivot. k is a number of element smaller than the pivot.
  T(k) -> recursion relation for elements right of pivot.
  ?(n) -> It is for partition process.
• Time complexity of Quick Sort is O(n*logn) in best and average case and O(n*n) in the worst case.
  Worst case is one when all elements of given array are smaller than pivot or larger than the pivot.
• Worst case can be easily eliminated by choosing random element as a pivot or best way is to choose median element as a pivot.
• It is an in-place sorting algorithm as it requires small additional storage space.
• Quick Sort is not a stable sort, which means the “equal” elements may not appear in the same order in the sorted array as they were in the unsorted array.

Let’s understand it with an example in which our last element is pivot-

Since a picture speaks a thousand words. Just carefully read the steps in the image below and you will be able to visualize the concept of this algorithm.
The following diagram is from hackerrank which shows partitioning of array choosing the last element of array as a pivot.
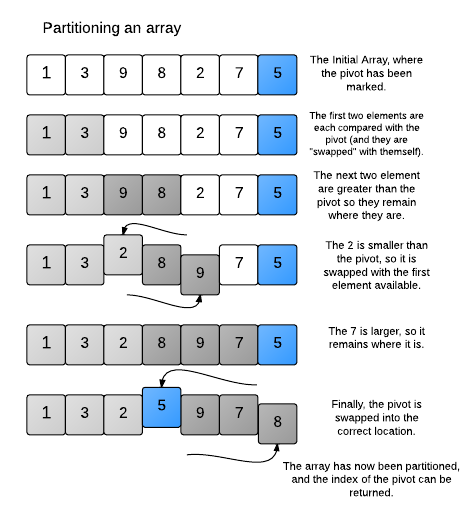Working of partition function:
Here the last element is chosen as a pivot. We initialize our partition index as the first element of the array. Then we compare each element with pivot from beginning, if the element is less than the pivot, so we will swap the element with the element at the partition index and increment the partition index . At the end, we will get our partitioned array in which all elements smaller than pivot will appear to the left of pivot and elements greater than pivot to its right in the array.

Pseudocode of Quick Sort

QUICK-SORT(A,start,end)
    if start < end
        pIndex = PARTITION(A,start,end)
        QUICK-SORT(A,start,pIndex-1)
        QUICK-SORT(A,pIndex+1,end)
end func
/*To sort an entire array A,
the initial call is QUICK-SORT(A,0,A.length-1)*/

//partitioning the array with respect to pivot.
PARTITION(A,start,end)
    pivot = A[end]
    pIndex = start
        for i = start to end-1
           if A[i] < pivot
               swap A[i] with A[pIndex]
                pIndex=pIndex+1
    swap A[pIndex] with A[end]
   return pIndex
end func

Asymptotic Analysis of Quick Sort

• General relation for quick sort: T(n) = T(k) + T(n-k-1)+ ?(n).
• Best Case: T(n)= 2T(n/2)+ ?(n). Time complexity: O(n*logn)
  Best case occurs when a middle element is chosen as a pivot. It means a number of elements smaller than pivot are equal to the number of elements greater than the pivot.
• Average Case: T(n)= T(n/3)+T(2n/3)+ ?(n). Time complexity: O(n*logn)
  Average case can be considered when partition puts O(n/3) elements in one set and O(2n/13) elements in other set.
  Worst Case: T(n)= T(n-1)+ ?(n). Time complexity: O(n*n)
• Worst case occurs when all elements of given array are smaller than pivot or larger than pivot. Ex- Suppose array is already sorted and we choose the last element as a pivot.
• Algorithmic Paradigm: Divide and Conquer
• Space Complexity: O(n*logn ) in an average case.
• Sorting In Place: yes
• Stable: no

Implementation of Quick Sort in C programming language

/* C implementation QuickSort */
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
// Swapping numbers using call by reference
void swap(int* x, int* y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}

/* In this function last element is chosen as pivot,
   then elements are arranged such that,all elements
   smaller than pivot are arranged to left of pivot
   and all greater elements to right of pivot */
int partition(int A[], int start, int end)
{
    int pivot = A[end];    // choosing pivot element
    int pIndex = start;  // Index of first element
    int i;
    for (i=start; i<=end-1; i++)
    {
        /* If current element is smaller than or
         equal to pivot then exchange it with element
         at pIndex and increment the pIndex*/
        if (A[i]<= pivot)
        {
            swap(&A[pIndex], &A[i]);
            pIndex=pIndex+1;
        }
    }
    /*exchange pivot with pIndex at the completion
    of loop*/
    swap(&A[pIndex], &A[end]);
    return pIndex;
}

 /* The main function that implements QuickSort
    A[] --> array to be sorted,
    start  --> Starting index,
    end  --> Ending index */
void quick_sort(int A[], int start, int end)
{   int diff=(end-start);
    if (start < end)
    {
        /* p is pivot index after partitioning*/
        int p = partition(A, start, end);
        // Recursively sort elements left of pivot
        // and elements right of pivot
        quick_sort(A, start, p-1);
        quick_sort(A, p+1, end);
    }
}

/*  function to print an array */
void print_array(int A[], int size)
{
    int i;
    for (i=0; i < size; i++)
        printf("%d ", A[i]);
    printf("
");
}

// Driver program to test above functions
int main()
{
    int A[] = {1, 3, 9, 8, 2, 7, 5};
    int n = sizeof(A)/sizeof(A[0]);

    printf("Unsorted array: ");
    print_array(A, n);
    printf("
");

    quick_sort(A, 0, n-1);

    printf("Sorted array: ");
    print_array(A, n);
    return 0;
}

Output:-
Unsorted array:  1 3 9 8 2 7 5 
Sorted array:    1 2 3 5 7 8 9

Partition function for random element as pivot

In the above code where we choose the last element as a pivot, it may lead to the worst case of quick sort. So, we can eliminate this case by choosing random element as a pivot. Here is a partition function for a random element as a pivot.

//C code for random pivot partition function.
/*Here we just found random index and swap that number with last element
  and then just done partitioning in the same way as we have done for 
  last element as pivot.*/

int random_partition(int A[], int start, int end)
{
    int diff=(end-start);
    //rand() function to get random index between our start and end index
    int randNumb=(int)(((double)(diff+1)/RAND_MAX) * rand() + start);

   //replace random index number with last element.
    swap(&A[end], &A[randNumb]);

    // Then following same logic for partition
    int pivot = A[end];    // choosing pivot element
    int pIndex = start;  // Index of first element
    int i;
    for (i=start; i<=end-1; i++)
    {
        /* If current element is smaller than or
         equal to pivot then exchange it with element
         at pIndex and increment the pIndex*/
        if (A[i]<= pivot)
        {
            swap(&A[pIndex], &A[i]);
            pIndex=pIndex+1;
        }
    }
    /*exchange pivot with pIndex at the completion
    of loop*/
    swap(&A[pIndex], &A[end]);
    return pIndex;
}

Implementation of Quick Sort in Java programming language

package com.codingeek;

import java.util.Arrays;

/* Java implementation QuickSort */
public class QuickSort {
	int A[];
	
	/* In this function last element is chosen as pivot,
	   then elements are arranged such that,all elements
	   smaller than pivot are arranged to left of pivot
	   and all greater elements to right of pivot */
	
 int partition(int start, int end)
 {
     int pivot = A[end]; // choosing pivot element
     int pIndex = start; // Index of first element
    
     for (int i=start; i<=end-1; i++)
     {
    	 /* If current element is smaller than or
         equal to pivot then exchange it with element
         at pIndex and increment the pIndex*/
         if (A[i] <= pivot)
         {
        	 // swap A[pIndex] and A[i]
        	 swap(pIndex,i); 
             pIndex=pIndex+1;
         }
     }
     // swap A[pIndex] and A[end] (or pivot)
     swap(pIndex,end);
     return pIndex;
 }

 /* The main function that implements QuickSort
 arr[] --> array to be sorted,
 start  --> Starting index,
 end  --> Ending index */
 void sort(int arr[], int start, int end)
 {
    this.A=arr;
	 if (start < end)
     {
         /* pi is partitioning index, A[pi] is 
           now at right place */
         int p = partition(start, end);

         // Recursively sort elements left of pivot
         // and elements right of pivot
         sort(A, start, p-1);
         sort(A, p+1, end);
     }
 }
 //function two swap two numbers.
 //we will pass index of array to swap
 private void swap(int i, int j) {
     int temp = A[i];
     A[i] = A[j];
     A[j] = temp;
 }

//Driver program to test above functions
 public static void main(String args[])
 {
     int arr[] = {1, 3, 9, 8, 2, 7, 5};
     int n = arr.length;
   //print unsorted array using Arrays.toString()
     System.out.print("Unsorted array: ");
     System.out.println(Arrays.toString(arr));
     
     QuickSort ob = new QuickSort();
     ob.sort(arr, 0, n-1);

     System.out.print("Sorted array: ");
   //print sorted array
     System.out.println(Arrays.toString(arr)); 
 }
}

Output:-
Unsorted array:  1 3 9 8 2 7 5 
Sorted array:    1 2 3 5 7 8 9

Quick sort is one of the fast and important sorting algorithms, which is widely used for commercial applications. Never use quick sort for applications which requires guaranteed response time. As a good programmer, you should be aware of this algorithm and it is fast sorting algorithm with time complexity of O(n log n) in an average case. Always use quick sort or merge sort for faster and efficient programming. The only disadvantage of quick sort is that its worst time complexity is O(n*logn). But, it has an advantage over merge sort as it is in-place sorting algorithm.

Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.

Keep Learning… Happy Learning.. 🙂

Recommended -