Graph – Introductions, Explanations and Applications
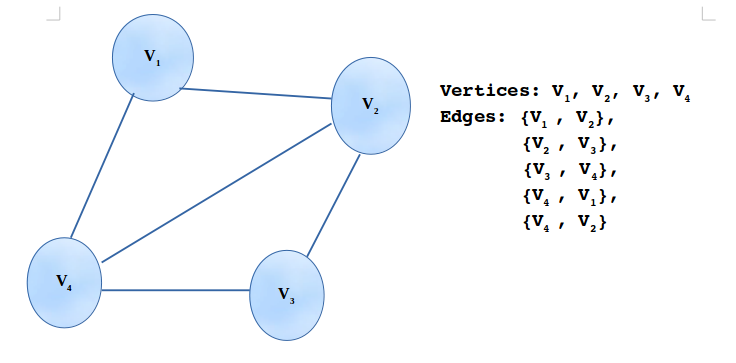
A graph is a data structure defined as G(V, E) where V is a set of nodes and E is set of edges.
Each edge is a pair of nodes like edge e1 = {v1, v2}, v1, v2 belongs to V(a set of vertices that form the graph). These vertices v1 and v2, are named as Endpoints.
These set of nodes also termed as Vertices or Points.
Graph Classification:
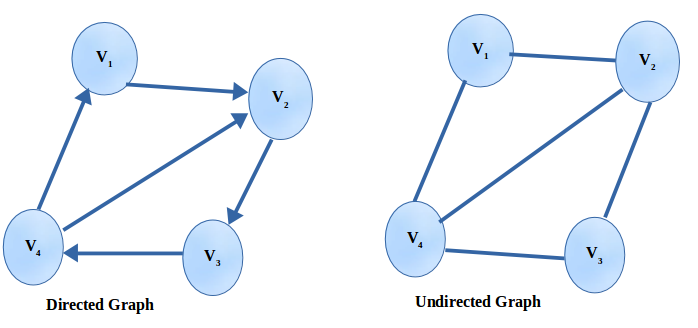
1. Directed graph and Undirected Graph
A Directed graph shows traversing direction between two nodes.
An Undirected graph shows traversing could be in any direction between two nodes.
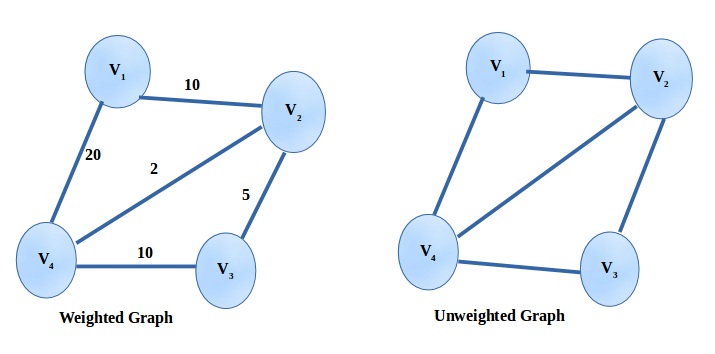
2. Weighted Graph and Unweighted Graph
In a weighted graph, all edges have some associated cost.
In an unweighted graph, there is no associated cost to the edges. It just tells whether the two nodes are connected or not.
3. Cyclic and Acyclic graph
If the graph is containing cycle then cyclic graph, otherwise, Acyclic.
A Cycle is a path that starts and end at the same vertex.

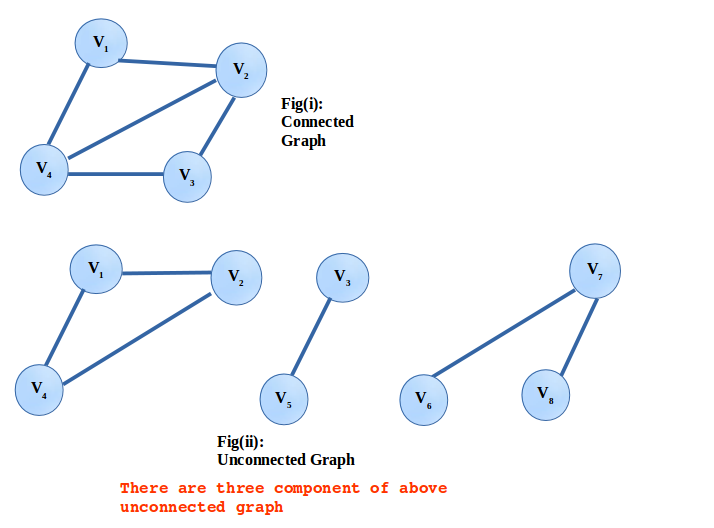
4. Connected and Unconnected graph
A Connected graph has all pairs of vertices connected by at least one path.
Failing the connected graph refers as an Unconnected graph. An unconnected graph is further defined as the maximum number of components where a component is a connected subgraph of the unconnected graph.
Importance of graph:
For representing any kind of network, graph data structure is used. Such as Telephone network, Transportation networks, Social networks like Facebook, Quora etc.
The newsfeed in Facebook, we can consider us as the root and all our adjacent vertices as our friends and so on.
In fact, Graph theory is a separate subject studied under mathematics. It has a very diverse application such as in Biochemistry, Electrical engineering, Computer science, Operational research and many more.
Terminologies:
1. Degree of a Node
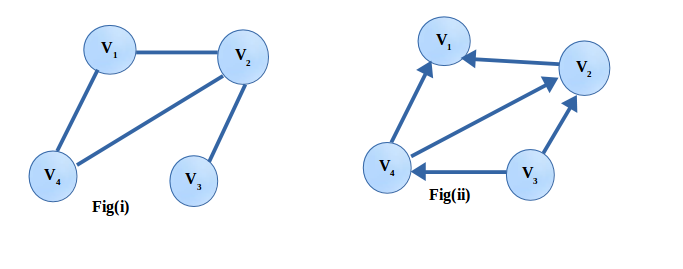
The degree of a node is the number of edges the node has. In fig(i) degree(v1) = 2, degree(v2) = 3; In fig(ii) degree(v2) = 3.
In a directed graph, there are two terms defined indegree and outdegree.
- Indegree – the number of edges to the node. Look at fig(ii), indegree(v1) = 2, indegree(v2) = 2, indegree(v3) = 0
- Outdegree – the number of edges from the node. outdegree(v1) = 0, outdegree(v2) = 1, outdegree(v3) = 2.
2. Path – It is a sequence of adjacent vertices. Path shows the connectivity of two vertices.

In fig(i) path between v4 and v3 is {v4-v2-v3 and v4-v1-v2-v3}. Similarly in fig(ii), path between v4 and v1 is {v4-v1 and v4-v2-v1}
3. Cycle – It is a path that starts and ends with same vertex.
4. Tree – It’s an acyclic graph.
5. Forest – It’s a disjoint set of trees.
6. Spanning Tree – A spanning tree is defined for a connected graph. It’s a subgraph that contains all the vertices.
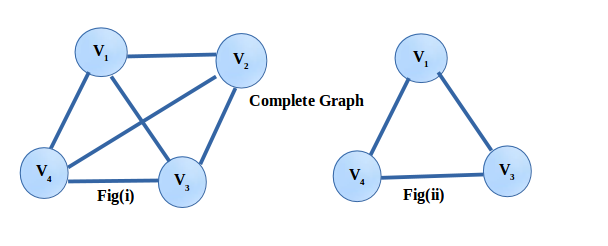
7. Complete graph – Such graph has all its vertices are connected to each other.
8. Sparse graph and Dense graph – Graph with relatively few edges are sparse graph and graph with a relatively very high number of edges are dense graph.
Applications:
Following are the broad applications of graph in computer science,
- Network of communication, e.g. Linkedin, telephone network
- Data organization such as in Database.
- The Flow of computation, like representing the flow of signals in an electronic circuit.
Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂