How to Insert, Delete and traverse a Binary Search Tree – Explanation with example
Binary search tree is a binary tree with following properties:
- Left sub tree of a node always contains lesser key
- Right subtree of a node always contains greater key
- Equal valued keys are not allowed
Sometime it is also referred as Ordered binary tree or Sorted binary tree.
With the aforementioned constraints, Searching gets faster. In best case searching takes Θ(logn), although the worst case leads to Ο(n) when the structure of the tree gets skewed. For eliminating the skewed based structure, further balanced binary search tree comes into the picture. Apart from searching, there are other advantages also such as in traversing, binary search tree is preferred.
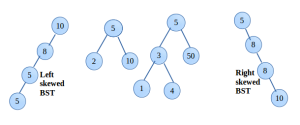
In the above shown binary search tree, first and last one are skewed BST.
Insertion and deletion in worst case takes O(n).
Operation on BST:
1. Insertion
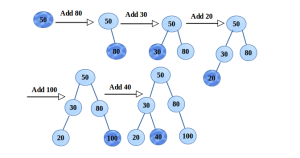
Say we have to build a BST of the keys, 50, 80, 30, 20, 100, 40. It can be clearly seen below, for inserting, first the key is compared is compared with the root, if smaller then goto Left subtree else Right subtree. The same step is repeated until all the keys are inserted.
2. Deletion
Deletion of a node is performed as follows,
- Deleting node has no child, therefore just delete the node(made to point NULL)
- Deleting node has 1 child, swap the key with the child and delete the child.
- Deleting node has 2 children, in this case swap the key with inorder successor of the deleting node. It should be noted, inorder successor will be the minimum key in the right subtree (of the deleting node).

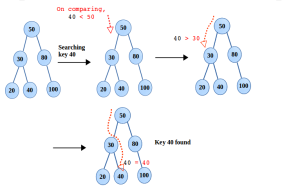
3. Searching
The steps follow in the insertion, are same followed here. Only difference is in comparison, if the key is not matched, repeat the steps till reached NULL. That says, desired key is not available in the BST.
4. Traversal
Interestingly, inorder traversal of any binary search tree outputs keys in non-decreasing order. This makes BST more useful in many implementations. The code mentioned below, inorder traversal is done by calling the function traverseInorder(root).
Code part also includes the preorder and postorder traversal. Read Tree Traversal techniques to learn more about them.
Implementation:
In C, using pointer based implementation similar to linked list, binary search is created.
#include<stdio.h>
#include<stdlib.h>
typedef struct node{
int key;
struct node *left;
struct node *right;
}Node;
/*for creating new node */
Node * newNode(int key){
Node *temp = (Node *)malloc(sizeof(Node));
temp->key = key;
temp->left = NULL;
temp->right = NULL;
return temp;
}
/*for inserting the key, newNode is the node needed to be inserted */
Node * insert(Node *p, Node *nwNode){
if(!p){
printf("Key %d\tinserted\n", nwNode->key);
return nwNode;
}
if(nwNode->key > p->key){
insert(p->right, nwNode);
if(!(p->right))
p->right = nwNode;
}
else{
insert(p->left, nwNode);
if(!(p->left))
p->left = nwNode;
}
return p;
}
/* for searching the key */
void search(Node *p, int searchKey){
if(!p){
printf("No key found for value - %d.\n", searchKey);
return ;
}
if(p->key == searchKey){
printf("Key %d\tfound\n", searchKey);
}
else if(p->key < searchKey)
search(p->right, searchKey);
else
search(p->left, searchKey);
}
/* inorder successor in BST will be the minimum key in right subtree */
Node * getInSuccessor(Node *p){
while(p->left != NULL)
p = p->left; //this will give the minimum key
return p;
}
Node * deletion(Node *p, int delKey){
struct node *temp;
if(!p){
printf("Unable to delete. No such key exists.\n");
return p;
}
else if(delKey > p->key)
p->right = deletion(p->right, delKey);
else if(delKey < p->key)
p->left = deletion(p->left, delKey);
/* executing else means get the key */
else{
/* node has one child or no child */
if(p->left == NULL){
temp = p->right;
free(p);
return temp;
}
else if(p->right == NULL){
temp = p->left;
free(p);
return temp;
}
/* node with two children, interchange with inorder successor */
temp = getInSuccessor(p->right);
p->key = temp->key;
p->right = deletion(p->right, temp->key); // Delete the inorder successor
}
return p;
}
/* Preorder traversal that outputs key in non-decreasing order*/
void traversePreorder(Node *p){
if(!p)
return ;
printf("%d ", p->key);
traversePreorder(p->left);
traversePreorder(p->right);
}
/* Inorder traversal that outputs key in non-decreasing order*/
void traverseInorder(Node *p){
if(!p)
return ;
traverseInorder(p->left);
printf("%d ", p->key);
traverseInorder(p->right);
}
/* Postorder traversal that outputs key in non-decreasing order*/
void traversePostorder(Node *p){
if(!p)
return ;
traversePostorder(p->left);
traversePostorder(p->right);
printf("%d ", p->key);
}
int main(void){
Node *root = NULL;
root = insert(root, newNode(50));
insert(root, newNode(80));
insert(root, newNode(30));
insert(root, newNode(40));
insert(root, newNode(20));
insert(root, newNode(100));
search(root, 50);
search(root, 10);
Node *newRoot = deletion(root, 50);
if(newRoot){
printf("Successfully deleted node. Now tree root node is - %d.\n", newRoot->key);
}
search(root, 50);
printf("Preorder Traversal: ");
traversePreorder(root);
printf("\nInorder Traversal: ");
traverseInorder(root);
printf("\nPostorder Traversal: ");
traversePostorder(root);
return 0;
}
Output:-
Key 50 inserted
Key 80 inserted
Key 30 inserted
Key 40 inserted
Key 20 inserted
Key 100 inserted
Key 50 found
No key found for value - 10.
Successfully deleted node. Now tree root node is - 80.
No key found for value - 50.
Preorder Traversal: 80 30 20 40 100
Inorder Traversal: 20 30 40 80 100
Postorder Traversal: 20 40 30 100 80
Knowledge is most useful when liberated and shared. Share this to motivate us to keep writing such online tutorials for free and do comment if anything is missing or wrong or you need any kind of help.
Keep Learning… Happy Learning.. 🙂