Multiple ways to represent a Graph
A graph can have several ways of representation, each one has their respective uses. However, the most commonly used are the Adjacency list and Adjacency Matrix.
Read about graph – Graph – Introduction, Explanations, and Applications
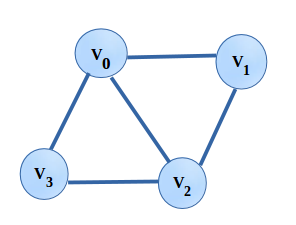
Representation of Graph:
Graph representation is done in following ways-
- Adjacency Matrix
- Adjacency List
- Adjacency Set
- Edge List
1. Adjacency Matrix
A Matrix VxV is created, where V denotes the number of vertices in the graph. Considering all the vertices are numbered as 0 to V-1(or 1 to V).
Endpoint(i, j as i, j ∈ V) of every edge will be the corresponding matrix entry [i][j].
Time complexity to access any edge is O(V2) and so is the space complexity. However, it’s easy to implement and very efficient whenever we have a dense graph. The adjacency matrix representation of the above graph will be-
Here vertices V0, V1, V2 and V3 are taken as 0, 1, 2 and 3 respectively in the matrix. All the zero entries denote as no edges between those vertices. As our graph contains no self-loop to any vertex, hence, all the principal diagonal entries are zeros.
Implementation:
The following implementation of the adjacency matrix of the graph is for an undirected graph. In this example, a dynamic 2D array is used.
#include<stdio.h>
#include<stdlib.h>
typedef struct graph{
int nVertices; //number of vertices in the graph
int nEdges; //number of edges in the graph
int **adjMatrix;
}Graph;
void printGraph(Graph *);
Graph * createAdjMatrixOfGraph(Graph *);
/* this will create Adjacency matrix of the undirected graph graph */
Graph * createAdjMatrixOfGraph(Graph *g){
int i, u, v;
g = (Graph *)malloc(sizeof(Graph));
printf("Enter the number of Vertices and Edges:");
scanf("%d%d", &g->nVertices, &g->nEdges);
g->adjMatrix = (int **)malloc(sizeof(int *) * g->nVertices);
for(i = 0; i < g->nVertices; i++)
g->adjMatrix[i] = (int *)malloc(sizeof(int) * g->nVertices);
for(i = 0; i < g->nEdges; i++){
printf("Reading the endpoints of an edge(u v):\n");
scanf("%d %d", &u, &v);
g->adjMatrix[u][v] = 1;
g->adjMatrix[v][u] = 1;
}
return g;
}
void printGraph(Graph *g){
int i, j;
printf("\n***Adjacency Matrix of Graph***\n");
for(i = 0 ; i < g->nVertices; i++ ){
printf("\n\t");
for(j = 0 ; j < g->nVertices; j++ ){
if( g->adjMatrix[i][j] ){
printf("1 ");
}
else
printf("0 ");
}
}
}
int main(void){
Graph *g = NULL;
g = createAdjMatrixOfGraph(g);
printGraph(g);
return 0;
}
Output:-
Enter the number of Vertices and Edges:4
5
Reading the endpoints of an edge(u v):
0
1
Reading the endpoints of an edge(u v):
0
2
Reading the endpoints of an edge(u v):
0
3
Reading the endpoints of an edge(u v):
3
2
Reading the endpoints of an edge(u v):
1
2
***Adjacency Matrix of Graph***
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 02. Adjacency List
As the name justified list, this form of representation uses list. A separate linked list for each vertex is defined. Each edge is shown in the form of connected vertices via linked list. The time complexity is O(E+V) and is best suited whenever have a sparse graph.
The adjacency list representation of the above graph is,

Implementation:
An array of linked list structure is created for the implementation.
#include<stdio.h>
#include<stdlib.h>
/*representing a node */
typedef struct linkedListNode{
int vertex;
struct linkedListNode *next;
}listNode;
typedef struct adjecencyList{
listNode *head;
}adjList;
typedef struct graph{
int nVertices; //number of vertices in the graph
int nEdges; //number of vertices in the graph
adjList *array; // array of adjacency list
}Graph;
Graph *addEdge(Graph *, int , int );
Graph *createAdjListOfGraph(Graph *);
void printGraph(Graph *);
/* this will create Adjacency list of the undirected graph graph */
Graph *createAdjListOfGraph(Graph *g){
int i, u, v;
g = (Graph *)malloc(sizeof(Graph));
printf("Enter the number of Vertices and Edges:");
scanf("%d%d", &g->nVertices, &g->nEdges);
/*size of array of adjacency list will be total number of vertices */
g->array = (adjList *)malloc(sizeof(adjList) * g->nVertices);
for(i = 0; i < g->nVertices; i++)
g->array[i].head = NULL;
for(i = 0; i < g->nEdges; i++){
printf("Reading the endpoints of an edge(u v):\n");
scanf("%d %d", &u, &v);
g = addEdge(g, u, v);
}
return g;
}
/* adding edge whose endpoints are u and v*/
Graph *addEdge(Graph *g, int u, int v){
listNode *temp1, *temp2;
temp1 = (listNode *)malloc(sizeof(listNode));
temp1->vertex = v;
temp1->next = g->array[u].head;
g->array[u].head = temp1;
temp2 = (listNode *)malloc(sizeof(listNode));
temp2->vertex = u;
temp2->next = g->array[v].head;
g->array[v].head = temp2;
return g;
}
void printGraph(Graph *g)
{
int i;
printf("\n***Adjacency list of the graph:***");
for (i = 0; i < g->nVertices; i++)
{
listNode *temp = g->array[i].head;
printf("\nVertex %d", i);
while (temp)
{
printf("->%d", temp->vertex);
temp = temp->next;
}
}
}
int main(void){
Graph *g = NULL;
g = createAdjListOfGraph(g);
printGraph(g);
return 0;
}
Output:-
Reading the endpoints of an edge(u v):
0
1
Reading the endpoints of an edge(u v):
0
2
Reading the endpoints of an edge(u v):
0
3
Reading the endpoints of an edge(u v):
2
1
Reading the endpoints of an edge(u v):
2
3
***Adjacency list of the graph:***
Vertex 0 -> 3 -> 2 -> 1
Vertex 1 -> 2 -> 0
Vertex 2 -> 3 -> 1 -> 0
Vertex 3 -> 2 -> 0
3. Adjacency Set
It’s pretty similar to adjacency list, the difference lies in the implementation. Each vertex referring its set of connected/adjacent nodes, that’s the approach both adjacency set and adjacency list follow.
4. Edge List
It’s the simplest way to represent a graph. Define an array edge[] of objects, where the object will be containing the endpoint of an edge. The number of edges will be the size of the array. In case, need to store the associated weight of the edge, add it to the object.
In C language, using structure we can create the object as
struct Edge{
char u;
char v;
int cost;
}
struct Edge edge[];
However, while solving the problems under the graph, this representation is not of much helpful. Though it takes O(E) time on accessing, yet rarely used.
So that’s all for this tutorial. Hope this helps and you like the tutorial. Do ask for any queries in the comment box and provide your valuable feedback.
Do not forget to SHARE and SUBSCRIBE.
Keep Coding!! Happy Coding!! 🙂
